Introducing Sunscreen's ZKP compiler

Ravital Solomon

Aug 24, 2023 • 8 min read

This is a two part series! In part i, we looked at how ZKPs and FHE fit together and how existing ZK infrastructure falls short when working with FHE. In this part, we’ll be diving into how Sunscreen’s ZKP compiler works.

Our ZKP compiler is aimed primarily at developers who want to work with both FHE and ZKPs. Anyone can use our compiler–whether they’re new to the ZK space or seasoned experts who want to create their own gadgets. We have tried to abstract away as much cryptography as we could while keeping the API as consistent as possible with that of our FHE compiler. You don’t have to use FHE to get value out of our ZKP compiler though! As we expand support to other proof systems, our compiler can be used to create and serialize ZKP programs more generally.

Going from program idea to ZKP

ZKPs are an amazing innovation, opening up interesting use cases from private transactions to decentralized identity and zk-rollups.

However, the process of creating a SNARK can be quite difficult for most developers. Let’s take a look at how this works.

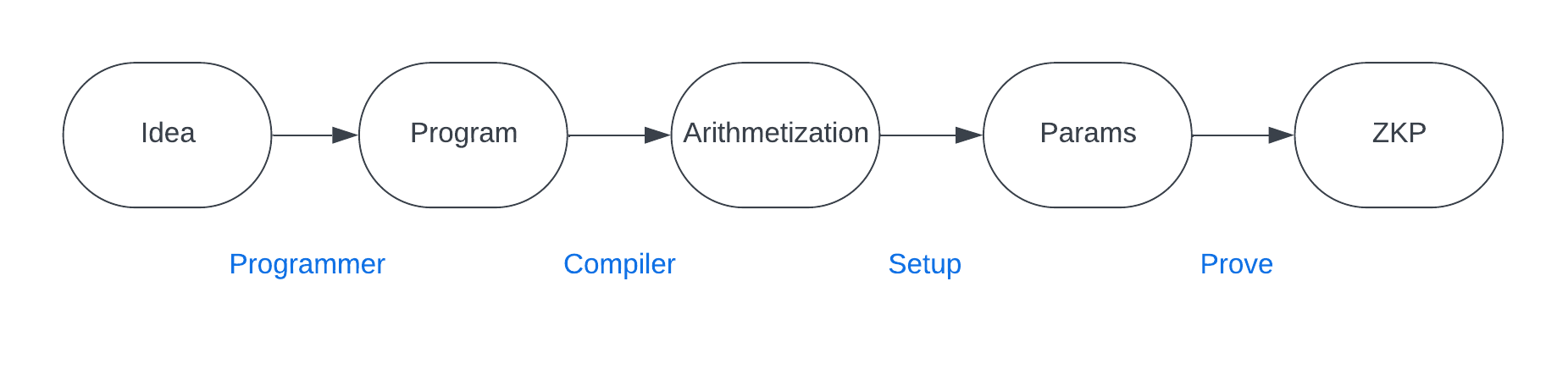
Image adapted from Berkeley's online ZKP course.

"Idea" : The developer has an idea for an application or program he wants to create that requires proving some relations over private data.
"Program" : The developer translates his application idea into a program written in some high level programming language like Python or Rust.
"Arithmetization" : The developer needs to translate his program into a format that can be used in a ZKP. This requires thinking about the program–specifically the parts involving relations over private data–in terms of circuits and constraints (conditions we want to impose on our inputs) instead. As part of this, the developer will need to choose a particular arithmetization scheme (such as R1CS).
"Params" : Once the developer has translated the relevant part of his program into circuits and constraints, he can feed that into the setup process of a ZKP to generate parameters (e.g. reference string) needed in the proving and verifying algorithms.
"ZKP" : Finally, the developer has a ZKP statement ready to go that others can interact with (i.e. to create proofs and verify proofs).

So where does a compiler come in?

Well, it helps automate the process of translating the relevant part of your program into a format that can then be used in a ZKP—setting up the circuits and constraints for you behind the scenes according to the chosen arithmetization!

What does our ZKP compiler offer?

An important consideration in building our ZKP compiler was deciding if we wanted to create our own language or a DSL embedded within an existing programming language. We chose to go with a Rust-based DSL as our FHE compiler follows the same format.

We have designed our compiler in a modular way so that we can plug in various proof systems in the backend and support different arithmetizations. For the initial version, we support R1CS with Bulletproofs as the proof backend.

While Bulletproofs are far from being the most efficient proof system out there, we chose it as it most easily links together with SDLP (i.e. can bind inputs across the commitments), is fairly fast (SDLP’s prover times dwarf that of Bulletproofs), and has a transparent setup process.

Two advanced features in our ZKP compiler that we’d like to call attention to are gadgets and custom ZKP types—both of which will become quite useful once we start linking together the FHE and ZKP compilers. We won't go into detail about them here as we'll share more about them in a later article.

Using Sunscreen's ZKP compiler

Now for the good parts! We’ll dive into how to create ZKP programs using Sunscreen’s compiler.

The developer creates a ZKP program (i.e. writing a Rust function with certain restrictions using the #[zkp_program] attribute).
- He specifies which inputs will be public vs. private (using #[public] and #[private] attributes).
- He specifies the relation that the prover is trying to show/the verifier will need to check. As part of this process, the developer has access to two types of constraints: equality and comparisons (i.e. >, <, >=, <=).
We compile the ZKP program, specifying the proof backend (e.g. Bulletproofs). Once compiled, the prover and verifier can interact with and use the compiled ZKP program.
Prover creates a proof using the compiled ZKP program, passing in the public inputs, along with their private inputs (i.e. witness). The prover and verifier will need to agree on the public inputs; how this is done in practice is application-dependent (e.g. data comes from a previous block in the chain, system parameters).
Verifier can check a given proof.

Let’s look at a simple example of the above workflow! In the program below, we’ll want to create a ZKP program that proves x is on a given list (without revealing which element it is on the list). For simplicity, we'll just look at a list containing two elements.

use sunscreen::{
     bulletproofs::BulletproofsBackend,
     types::zkp::{BulletproofsField, Field},
     zkp_program, zkp_var, FieldSpec, Error, ZkpProgramFnExt
 };

#[zkp_program]
 fn either<F: FieldSpec>(
     #[private] x: Field<F>, // Prover’s private inputs (i.e. witness)
     #[public] y: Field<F>, // public data
     #[public] z: Field<F>, // public data
 ) {
     let zero = zkp_var!(0);
     let poly = (y - x) * (z - x);
     poly.constrain_eq(zero); // if x=y or x=z then (x-y)*(x-z)=0 
 }

There are many different proof systems out there with various tradeoffs in terms of efficiency. How might we write our program generically so that we can compile it to various backend proof systems? We'll do this with the generic type parameter F:FieldSpec.

Next, notice that either looks just like any other Rust function, except for a few extra attributes. The top level attribute #[zkp_program] is where the magic happens–this declares your function as a ZKP program that can be compiled. Each program argument is either public (#[public]) or private (#[private]) depending on whether the argument should be hidden from the verifier. Since we’re working over a field, we’ll need to specify that the inputs x, y, and z are actually field elements. To create a field element within a ZKP program function, we can use the zkp_var macro. Finally, how might we specify that poly (i.e. (y - x) * (z - x)) must be equal to 0? We use constrain_eq, the equality constraint.

fn main() -> Result<(), Error> {
    let either_zkp = either.compile::<BulletproofsBackend>()?;
    let runtime = either.runtime::<BulletproofsBackend>()?;

    let x = BulletproofsField::from(64);
    let y = BulletproofsField::from(64);
    let z = BulletproofsField::from(1000);

    // Generate a proof that x is equal to either y or z
    let proof = runtime
        .proof_builder(&either_zkp) // compiled ZKP program
        .private_input(x)           // private inputs
        .public_input(y)            // public inputs
        .public_input(z)
        .prove()?;

    // Verify the proof
    runtime
        .verification_builder(&either_zkp) // compiled ZKP program
        .proof(&proof)                     // proof created by prover
        .public_input(y)                   // public inputs
        .public_input(z)
        .verify()?;

    Ok(())
}

Next, we’ll compile our ZKP program, specifying which proof backend we want to use (Bulletproofs). For the prover and verifier to interact with the ZKP program, we’ll need a ZkpRuntime. Once we have a runtime, the prover and verifier are ready to create and verify proofs, respectively.

If you’d like to try out our ZKP compiler before installing it, we offer a playground.

Extensive documentation can be found here.

A preview into "Short Discrete Log Proofs for FHE and Ring-LWE Ciphertexts" (SDLP)

Let’s take a closer look at this proof system as it’s fairly niche and serves a unique role for us. Feel free to skip this section if you’ve already had your daily dose of math.

If you’re worked with SNARKs, you’ve likely heard of groups and fields. However, we’ll be interested in rings when working with FHE. Rings can be thought of as an intermediary object between groups and fields. Whereas groups have a single operation defined on them and fields have two operations (+, *) with a guarantee of commutativity and inverses, rings have two operations (+, *) but with no guarantee that multiplication is commutative or that multiplicative inverses exist. We’ll be interested in a special type of ring involving polynomials–if you’d like to learn more about how arithmetic works in this ring, please see here.

FHE ciphertexts generally satisfy the following equation (i.e. can be written in the following format):

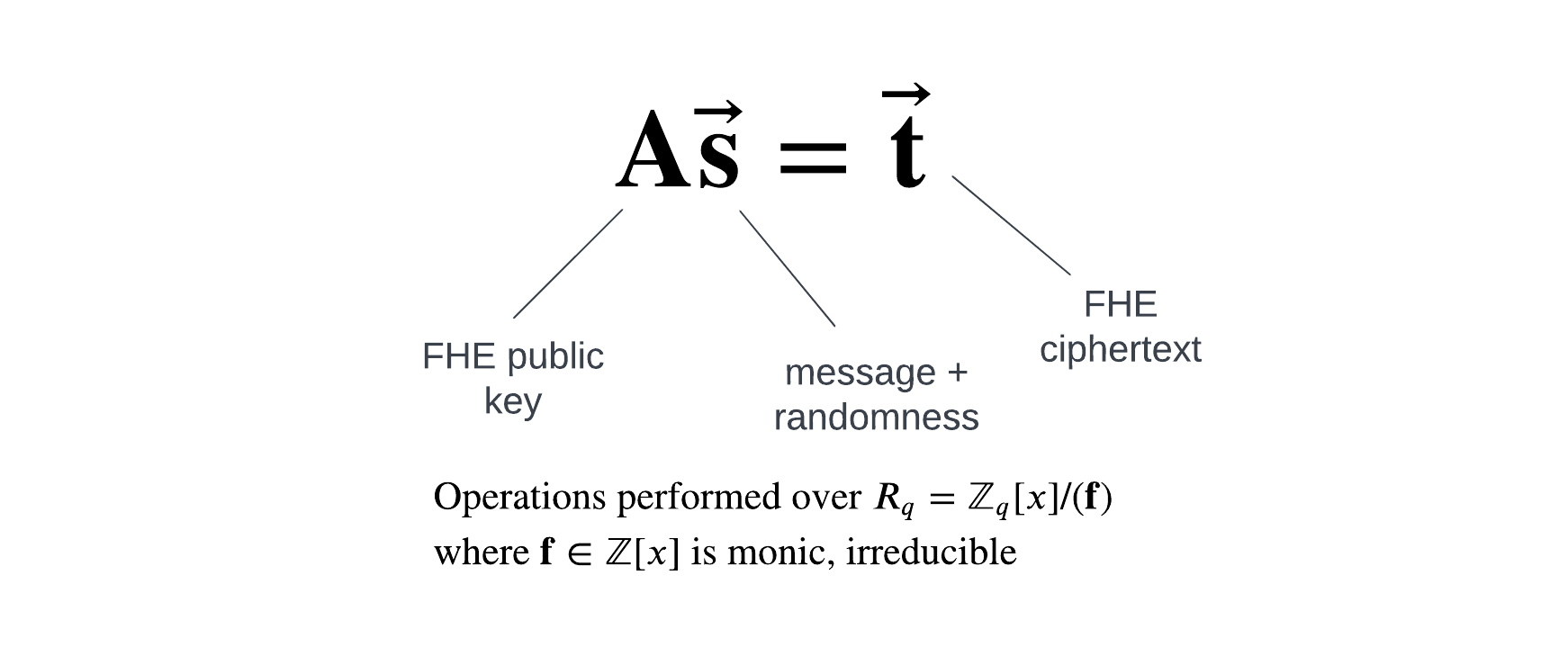
In ZK terminology, the vector s will be the “witness.” The prover will need to show that they have a vector s satisfying the above equation, where the noise/randomness is “small”, and such that the message coefficients are less than the plaintext modulus of the FHE scheme.

A nice property of SDLP is that the setup process is transparent. Proofs are logarithmic in the size of the witness (concretely, this leads to proofs around the single digit kilobyte range for most FHE ciphertexts). In practice, proofs generally take 10-20s to create on consumer laptops but verification times are challenging to keep low (i.e. <1s on a large machine).

The key idea of the proof system is to create a Pedersen commitment to the coefficients in the vector s and rely on elliptic curve-based cryptography to get smaller proofs than possible with existing lattice-based proof systems. Thus, we’ll need a group $ G $ of order $ p $ such that the discrete logarithm problem is hard. In practice, $ p >> q $, the modulus used in the ring for FHE.

Almost every step in the proof is parallelizable so we can take advantage of multiple cores when available. Additionally, we can use GPU acceleration for scalar inversion, scalar multiplication, and multi-scalar multiplication (along with implementing Pippenger’s algorithm). A lot of this work has already been done on our part.

Our technical work doesn’t end there though. To use SDLP with SEAL’s implementation of the BFV fully homomorphic encryption scheme, we need to ensure encryption is implemented in a linear fashion (so that a ciphertext indeed satisfies the matrix-vector equation $ \mathbf{A}\vec{\mathbf{s}} = \vec{\mathbf{t}} $). It turns out that SEAL has added in some optimizations so that encryption is no longer linear. We’ve had to alter SEAL’s implementation of BFV to make encryption linear again. Additionally, SDLP uses fixed bounds for the witness but there is no reason in practice that we would have to do this. In fact, if we are able to support mixed bounds then we can get better concrete performance (for certain cases) and correctness guarantees.

We are still working on linking together the SDLP and Bulletproofs proof systems.

Connecting our FHE and ZKP compilers

Initially, our ZKP compiler will be offered on a standalone basis. What this means for the developer is that you cannot yet prove things about FHE ciphertexts using Sunscreen's ZKP compiler.

Our goal is to provide an experience where the developer can write a program in Rust, adding #[fhe_program(...)] and #[zkp_program] attributes as needed to let the compiler know which parts of the code need to be transformed into their FHE and ZKP equivalents.

API design is a challenge and it’s unclear how to best expose both SDLP and R1CS constraints to the developer at the same time. Community feedback will play a crucial role in helping determine what the best API is.

What's next for us

In the next two months, you’ll be able to sign up for access to our private testnet. So far, our priority has been on developers, but we don’t want to leave anyone out! We’ll also be providing a demo suite of apps to try out.

We’ll be sponsoring EthGlobal New York, with $5000 worth in prizes available from Sunscreen. Hackers will get first access to our private testnet and our demo suite of FHE apps. Ravital, Rick, and Ryan will be at Sunscreen’s own cocktail table so come say hi!

Finally, we’ve been working on our own custom implementation of TFHE to provide ultra fast comparisons and enable new applications. If you’re a developer interested in using FHE in your project, feel free to reach out to us for first access.